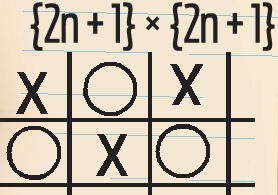Svoje nesporné nadanie si cibrí už od šiestich rokov a výsledkom sú pozoruhodné úspechy na medzinárodnom fóre. Marián Poturnay (18) chodí do oktávy na Gymnáziu Pierra de Coubertin v Piešťanoch. Len nedávno sa zúčastnil na Stredoeurópskej matematickej olympiáde MEMO (Middle European Mathematical Olympiad), kde v silnej konkurencii zažiaril.
Spomedzi 66 účastníkov sa piešťanský gymnazista umiestnil najlepšie zo všetkých reprezentujúcich Slovákov a získal striebornú medailu v individuálnej súťaži. „Matematika je pre mňa nevyčerpateľný zdroj fascinácie. Pocit, keď po dlhom čase nájdem riešenie nejakej zamotanej úlohy, je prenádherný a nenahraditeľný,“ hovorí o svojej láske Majo, ktorý sa chystá na tohtoročnú maturitu, no popri učení sa rád odreaguje aj hrou na gitare.
Úlohy na olympiáde boli tento rok náročné. „Namiesto výsledku išlo prevažne o dôkaz, teda o vysvetľovanie, prečo je to práve toľko,“ prezradil Marián a dodal, že musel niekoľkokrát robiť dôkazy aj na celú stranu. Mladý študent sa v minulom roku zúčastnil aj na Medzinárodnej matematickej olympiáde v Brazílii, kde skončil tretí.
Voľný čas väčšinou venuje riešeniu náročných úloh a vraj aj preto ešte nemá priateľku. „Zbožňujem matematiku a je jasné, že moje ďalšie štúdium bude matematického zamerania. Zostanem doma na Slovensku a rozhodol som sa pre bratislavský matfyz, teda FMFI UK,“ predstavil svoje plány Majo.
Medaily
1. miesto - Pytagoriáda na Slovensku
2. miesto - Memo v Poľsku
3. miesto - Medzinárodná matematická olympiáda v Brazílii
Úloha pre ,,kockáčov"
Pavol striedavo vpisuje krížiky a krúžky do políčok tabuľky (začína krížikom). Keď je tabuľka celá vyplnená, výsledné skóre spočíta ako súčet X + O, pričom X je počet riadkov obsahujúcich viac krížikov ako krúžkov a O je počet stĺpcov obsahujúcich viac krúžkov ako krížikov. Určte najvyššie možné skóre dosiahnuteľné pre tabuľku (2n+1)×(2n+1) v závislosti od prirodzeného čísla n.
Výsledky posielajte na tip@novycas.sk